[10000印刷√] 1/√1-x^2 積分 145547-1/1+x^2 積分 アークタンジェント
1 √ 1x2 dx⇒ 8 Z p x2 2xdx⇒ 9 Z 1 x2(1x2) dx⇒ 10 Z x2 √ 4−x2 dx⇒ 11 Z √ x √ 1−x dx⇒ 12 Z x3 √ 4x2 −1 dx⇒ 103 tion Integra by ts r a P We have already seen that recognizing the product rule can be useful, when we noticed that Z sec3 u secutan2 udu = secutanu As with substitution, we do not have to rely on微分積分I 演習問題 令和3 年5 月19 日(水) 番号: 氏名: 評価: 1 C3 級であるが, C4 級でない関数の例を挙げよ。 2 次の関数の導関数を求めよ。 (1) y = tan−1 1 x (x ̸= 0) (2) y =sin−11 √ 1x2 (x ̸= 0)(3) y = tan−1 1 √ x2 −1 (x > 1) (4) y =sin−11 x (x > 1)Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history
How To Integrate Dx X 2 A 2 3 2 Quora
1/1+x^2 積分 アークタンジェント
1/1+x^2 積分 アークタンジェント-公式(積分)‐ 1 ‐ 公式(積分) 不定積分の定義 ∫ f(x) dx = F(x)C () F′(x) = f(x) 基本的関数の微分の逆 ∫ 0 dx = C ∫ x dx = 1 1 x 1 C ( =n 1) ∫ 1 x dx = logjxjC ∫ ex dx = ex C ∫ ax dx = ax loga C ∫ sinx dx = cosxC ∫ cosx dx = sinxC ∫ 1 cos2 x dx = tanxC ∫ (1tan2 x) dx = tanxC ∫ 1 √を上積分,下積分とよんで,それらが一致するときに可積分といい,その値 を重積分という. このときには,あとで述べる広義積分の場合と異なり,関数を正負に分け る必要はない. 例4 (錐の体積) 簡単のため,底辺の長さが2,高さが1 である四角錐を考




Ex 7 4 2 Integrate 1 Root 1 4x2 Class 12 Ncert Ex 7 4
· 積分1/√1x^2の積分、1/ax^2の積分、2回の置換を行う この記事では、特定の1/√1x^2の積分について置換積分を2回行う方法で解説します。 また、置換積分を1回でのみ解ける簡略的な方法についても解説しています。曲線c0 の点a がわずかに動いて点a′ に至っ たとする。このときの曲線c0 を点a から点 a′ までの長さを∆t 、対応する曲線c 1 の点 b から点b′ までの長さを∆t とする。 ま た、角の増分を∆θ とする。 a a′ b b′ b′′ r ∆θ ∆t ∆t ∆t = ⌢ bb′= ⌢ bb′′ ⌢ b′′b′= ⌢ aa′ ⌢ b′′b′≒ ∆ · くろべえ JG1BGT の受け狙い人生 >> 数学,学校,旅行,単車,鉄道,囲碁,トロンボーン,ドラム,アマチュア無線 JG1BGT,CW(モールス), Always QRP CW
安倍 齊 著 「微積分の歩んだ道」 (森北出版) p.152、153 変分法にて最短距離を与える曲線の問題: 2定点 P(x 1 ,y 1 )、Q(x 2 ,y 2 )を結ぶ曲線 y=y(x)のうち、y(x)が連続微分可能条件を満21 年6 月3 日 微分積分学I・演習問題3 問題31 関数f(x) を次で定める f(x) = xp logx, x > 0, 0, x ≤ 0 (1) f(x) がx = 0 で連続であるような実定数p の範囲を定めよ (2) f(x) がx = 0 で微分可能であるような実定数p の範囲を定めよ 問題32 関数f(x) = (logx)2 のn 次導関数を求めよ 問題33 次の極限を求/08/08 · 回答数: 1 件 http//jawikipediaorg/wiki/%E5%86%86%E5%91%A8% によると、 π=∫ 1,11/√ (1x^2) dx π=2∫ 1,1√ (1x^2) dx π=∫ ∞,∞1/ (1x^2) dx ということですが、 ∫ 1,11/√ (1x^2) dx =2∫ 1,1√ (1x^2) dx
· 積分√1x^2の積分、√Ax^2の積分、置換と部分積分の両方で解く この記事では、√1x^2の積分について2通りの方法で解説します。 2通りの方法とは、置換積分と部分積分での方法で、好きな方で覚えていただくと良いと思います。 · 積分したらlog(x√xの2乗1)になって−1から1まで代入して2log(1√2)になる ベストアンサー:log(1√2)-log(1√2) =log{(1√2)/(1√2)} = 分母を有理化してくださいませ。 · 積分1/√1x^2の積分、1/ax^2の積分、2回の置換を行う この記事では、特定の1/√1x^2の積分について置換積分を2回行う方法で解説します。 また、置換積分を1回でのみ解ける簡略的な方法についても解説しています。



X 2 1 4x 2 Dx怎么积分 微思作业本




不定積分 Dx 搜索结果 哔哩哔哩 Bilibili
解 t = 1−x2 とおく dt = −2xdx より置換積分法を使うと I = ∫ (− 1 2 √ t) dt = − √ tC = − √ 1−x2 C (5) I = ∫ x x2 1 dx 解 t = x2 1 とおく dt = 2xdx より置換積分法を使うと I = ∫ 1 2t dt = logt 2 C = log(x2 1) 2 C (6) I = ∫ cosx sin2 x1 dx 解 t = sinx とおく dt = cosxdx より置換積分法を使うと I = ∫ 1 t2 1 · 検算用サイトです。 http//wwwwolframalphacom/input/?i=x%2F%281x%5E2%29%5E%281%2F2%29 別解です。 ∫ {x/√ (1x^2)}dx t=√ (1x^2)とおきます。 両辺を2乗して、 t^2=1x^2 両辺をxで微分して、 2t (dt/dx)=2x xdx=tdt よって、 ∫ {x/√ (1x^2)}dx =∫ {1/√ (1x^2)}xdx =∫ (1/t) (tdt) =∫ (1)dt =tC =√ (1x^2)C 1人 がナイス! しています · ∫e^(sinx)dx,被积函数e的sinx次幂的不定积分,请问它如何积出来?感谢!!! ∫e^(sinx) dx, 被积函数 e的sinx次幂 的不定积分,




对于似1 1 X 4 型的不定积分的总结 Erasernut 博客园




写真の問題で1 1 Yの積分と1 1 Xの積分がlog 1 Y Log 1 X になる理由 数学 教えて Goo
è ∫√ (1 x2 )2xdx = ∫√u du = 2/3 u3/2 C = 2/3 (1x2)3/2 C 計算積分的微分時,要先看積分的下限是否是常數,若不是就先換,換完後,確認積分的上限是否和dt一樣,不一樣就假設u=上限再算 計算積分時,題目若很醜,把比較醜的令為u, du=dx*x',再開始解題 · 数学・算数 ∫1/ a bcosx dx (a,b>0)の 不定積分の計算のしかたを教えてください。t = tan θ/2 とおいて計算をしました。 a = b のときは簡単に求められたので · この記事では、特定の 1/√1x^2の積分 について置換積分を2回行う方法で解説します。 また、置換積分を1回でのみ解ける簡略的な方法についても解説しています。 最後には、例題もありますので、例題を見ながら理解していただくのもおすすめです。




X 3 X 2 1 の不定積分 申し訳ありませんが 画像を作成しましたの 数学 教えて Goo



Evaluate Cosx 1 Ex Dx X P 2 P 2 Sarthaks Econnect Largest Online Education Community
· 对于黎曼可积的函数,改变有限个点的取值,其积分不变。 对于勒贝格可积的函数,某个测度为0的集合上的函数值改变,不会影响它的积分值。 你对这个回答的评价是? ∫arcsinxdx =xarcsinx∫x/√ (1x^2)dx =xarcsinx∫1/√ (1x^2)d (1x^2) =xarcsinx2√ (1x^2)C 反三角 · 数学 定積分∫1/√3→1√(1x^2)dx が解けません。 ∫1/√3→1√(1x^2)dx を解く問題なのですが、公式に当てはめて、 ∫√(1Arcsin(x)のTaylor展開 ∞ arcsin(x)=Σ (2n)!/{(n!)^2・(4^n)・(2n1)}・x^(2n1) n=0 y=arcsin(x) ・・・①




What Is The Integration Of 1 Xe X Quora




求不定积分 X 2 9 1 2 Dx X 雨露学习互助
不定積分 f(x) F(x)=∫f(x)dx (積分定数Cは省略) )ln axb ln x (ln x)/x (ln x)/x 2グリーンの定理の別証 {1{ 定理 Dをxy平面の有界な領域で,その境界Cは互いに交わら ない有限個の区分的にC1 級の単一閉曲線からなっているとする そのときDを含む開集合でC1 級の関数f(x;y);g(x;y)に対して ∫∫ D (@g @x @f @y) dxdy= ∫ C fdxgdy が成り立つ ここで, CにはDに対して正の向きをつけて1 有理関数の不定積分∫ 1/( x^21 ) dx= ( 1/2 )( log x1 log x1 )C∫ 1/( x^21 ) d



Evaluate The Integral Of 1 A Bx2 Stumbling Robot




对于似1 1 X 4 型的不定积分的总结 Erasernut 博客园
· 私は、数学は好きなのですが、どういうわけか、積分だけは大嫌いです。大学レベルの積分でも苦戦してしまうほど苦手なので、よく見かける基本的な関数の不定積分の解法をここにメモしておきます。 {1 cos^2y} = 1 / √{1 x^2}解析学B2講義・演習(平成18年度前期) — Lebesgue積分— 谷口 説男(九州大学大学院数理学研究院) (平成18年8月3日版) 0This note is °c 06 by Setsuo Taniguchi It may be used for personal or classroom purposes, but not for commercial解析学B2講義・演習 (平成19年度前期)— Lebesgue積分— 谷口 説男 (九州大学大学院数理学研究院) (平成19年7月12日) 0This note is °c 07 by Setsuo Taniguchi




1 X 2 1 積分5 Lnzikz




How To Integrate 1 Sqrt X 2 1 Youtube
積分Sの被積分関数がt1,・・・,tnについて対称であることから,n次元超立方体0,1^nをn!個の単体に分割して これらの結果を併わせると c(z)=Γ(jz1)/Γ(z1) となり,セルバーグの積分公式が証明されます. · 数学 積分∫0→1√(1x^2)dx=π/4 定積分∫0→1√(1x^2)dx=π/4 この計算の仕方が分かりません。 x=sinθとおく。dx=cosθdθ。x0→1がθ0→2 質問No · 10)∫1/√(1x^2) dx=arcsinxc 求不定积分的方法: 第一类换元其实就是一种拼凑,利用f'(x)dx=df(x);而前面的剩下的正好是关于f(x)的函数,再把f(x)看为一个整体,求出最终的结果。



1 X 2 A 2 Dxの計算 物理のかぎしっぽ




Integral Of 1 Sqrt 1 X 2 Substitution Youtube
· 9y=arcsinx y'=1/√1x^2 10y=arccosx y'=1/√1x^2 11y=arctanx y'=1/1x^2 12y=arccotx y'=1/1x^2 扩展资料 求导证明: y=a^x 两边同时取对数,得:lny=xlna 两边同时对x求导数,得:y'/y=lna 所以y'=ylna=a^xlna,得证 注意事项 1不是所有的函数都可以求导;問題3 x= sinθ (π/2 ≦ θ ≦ π/2) とすると dx = cosθdθ 1/√(1x^2)=1/cos 問4と6が問題ですね。これらの積分は大学の教養課程で解いておりましたので思い出しながら解きましたが、問4は中々思い出さず、数時間かかりました。 · 扩展资料 不定积分的公式 1、∫ a dx = ax C,a和C都是常数 2、∫ x^a dx = x^ (a 1)/ (a 1) C,其中a为常数且 a ≠ 1 3、∫ 1/x dx = lnx C 4、∫ a^x dx = (1/lna)a^x C,其中a > 0 且 a ≠ 1 5、∫ e^x dx = e^x C 6、∫ cosx dx = sinx C 7、∫ sinx dx = cosx C




高校数学 定積分の置換積分 3 問題編 映像授業のtry It トライイット




部分分式法求积分 求积分 部分分式法求详细过程 三人行教育网 Www 3rxing Org
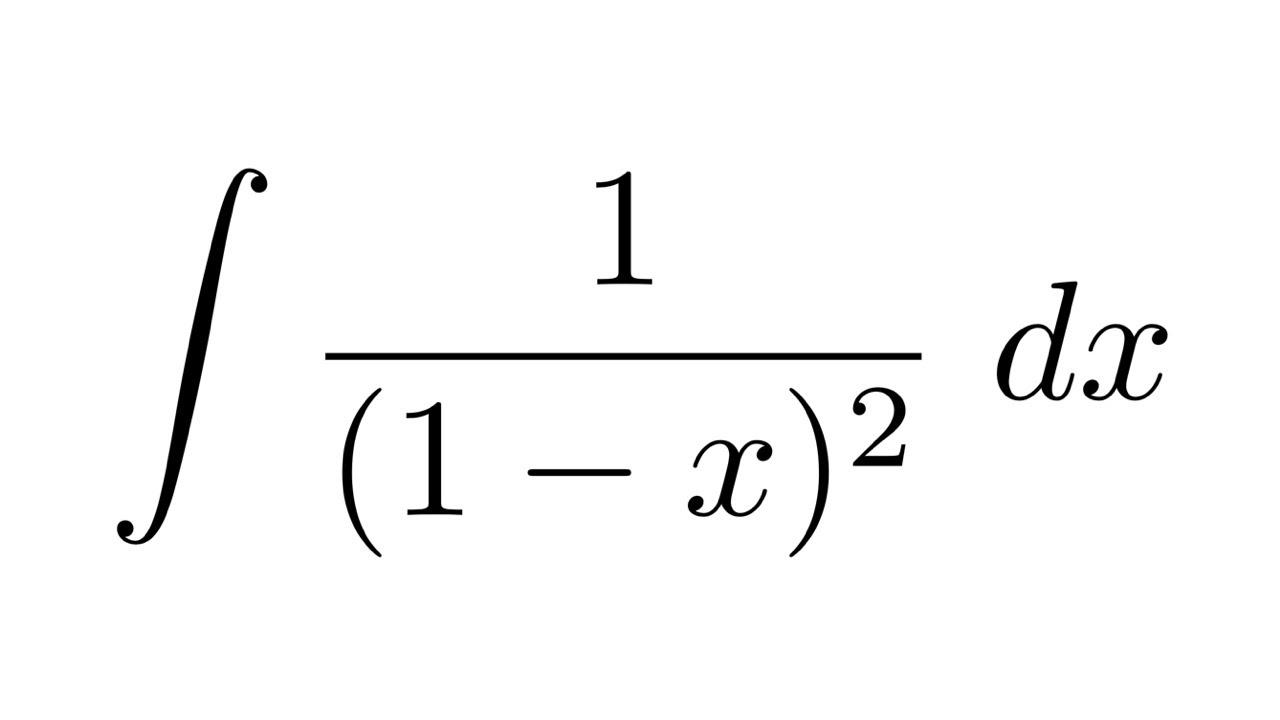



Integral Of 1 1 X 2 Youtube
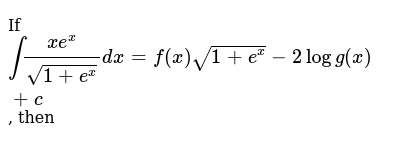



If Int Xe X Sqrt 1 E X Dx F X Sqrt 1 E X 2logg X C Then




高校数学 置換積分法 1 問題編 映像授業のtry It トライイット




How To Solve The Integral Of X 3 1 X 2 3 Quora




Gaussian Integral Wikipedia
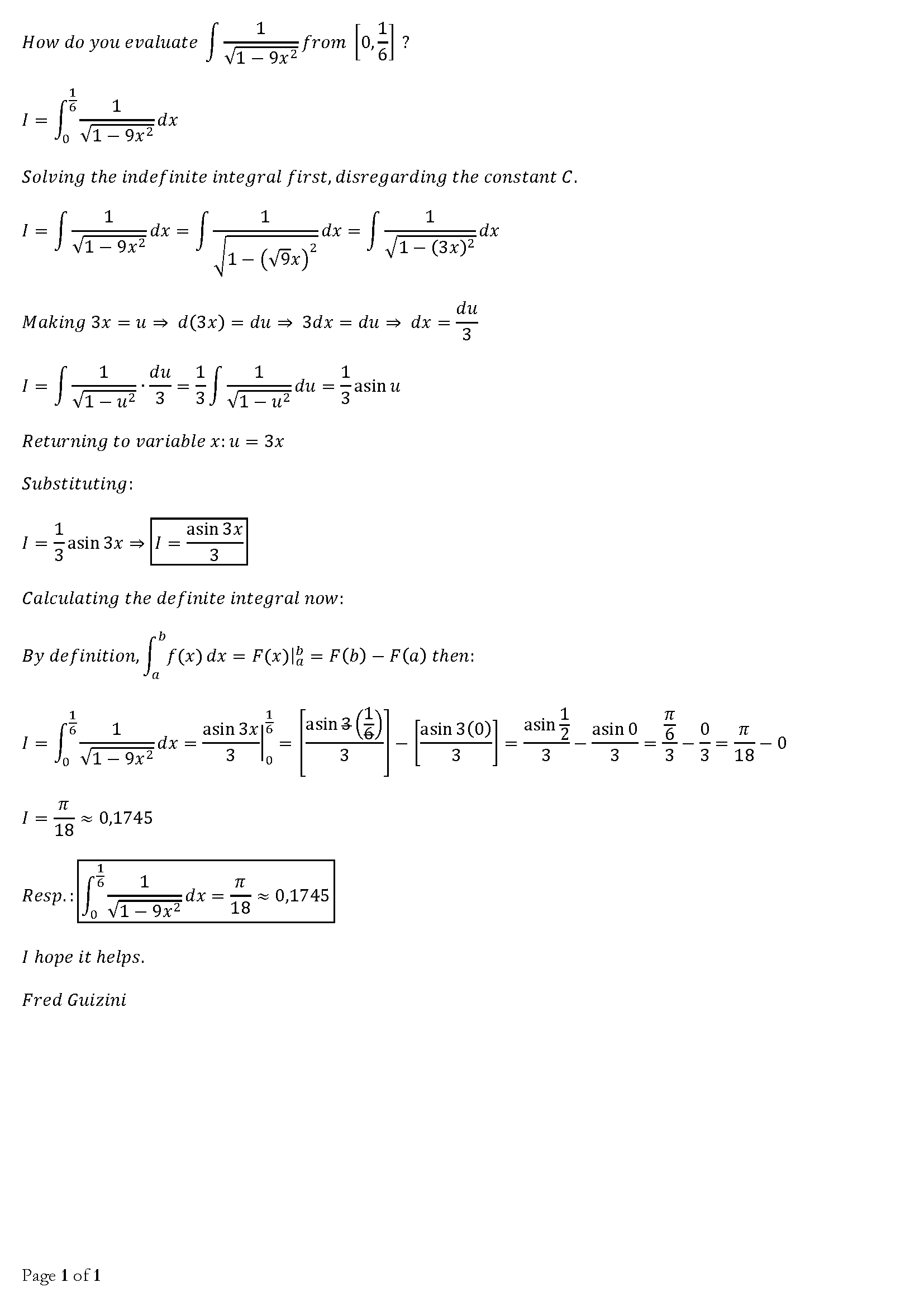



How Do You Evaluate Int1 Sqrt 1 9x 2 Dx From 0 1 6 Socratic



X2 1 X4 1求不定积分 不定积分 X4 1 X2 1 Dx




超越函数e X 2 的定积分 Norstc的博客 Csdn博客




大學高等數學 第三章第二講不定積分換元積分法 壹讀



1 X 2 の積分を教えてください 模範回答と Yahoo 知恵袋




Ex 7 4 2 Integrate 1 Root 1 4x2 Class 12 Ncert Ex 7 4
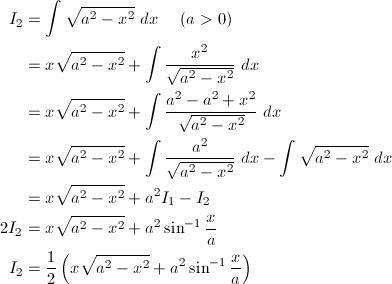



不定積分選 グラフ付き 数学自由研究




Int 1 Sqrt A 2 X 2 Dx Log X Sqrt X 2 A 2 C
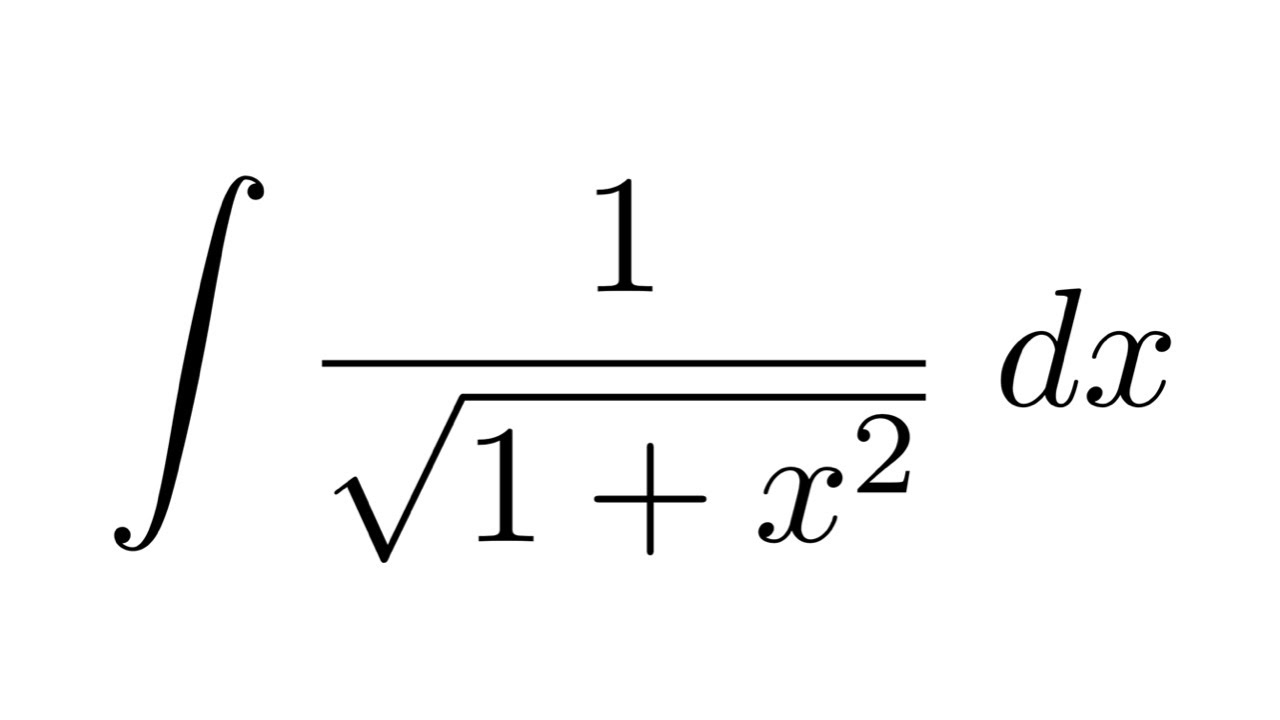



Integral Of 1 Sqrt 1 X 2 Substitution Substitution Youtube




用坐标系计算二重积分 D 根号 1 X 2 Y 2 Dxdy D X 2 Y 2 1 X 0 Y 0 雨露学习互助




交换下列累次积分的次序 时习社区



この定積分お願いしますx X 2 1 と置くことによって Yahoo 知恵袋




Integral Of 1 X 2 X Partial Fraction Decomposition Youtube




对于似1 1 X 4 型的不定积分的总结 Erasernut 博客园
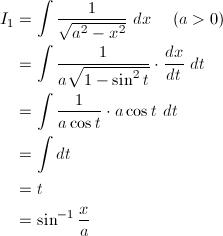



不定積分選 グラフ付き 数学自由研究



How To Integrate Dx X 2 A 2 3 2 Quora



1 X 2 A 2 Dxの計算 物理のかぎしっぽ




X平方乘根号下x平方加1 求微分根号下x的平方加一求




对于似1 1 X 4 型的不定积分的总结 Erasernut 博客园



X2 1 X4 1求不定积分 不定积分 X4 1 X2 1 Dx




1 X 29 X 2 Dx2 X 2 1 急 不确定积分 多次操作 详细过程 好加点o 365bet送彩金 365注单审核不能提款



1 X 1 Dx积分从1到3 作业 慧海网




1 根号下 1 X平方 立方乘以dx 求定积分 雨露学习互助
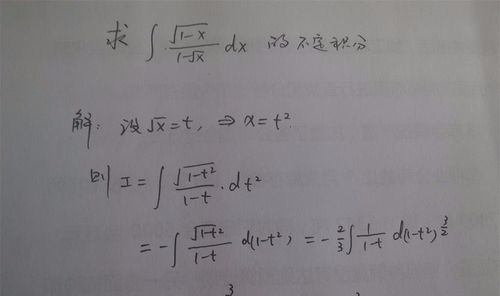



求 1 X与1 X的商的不定积分 搜狗指南




1 X 2 1 2 の不定積分がわかりません 1 X 2 1 2 の不定積分が 数学 教えて Goo



不定积分x E 1 Dx 计算不定积分 E的1 X次方 X平方dx




E的x次方定积分x乘以e的负x次方 定积分
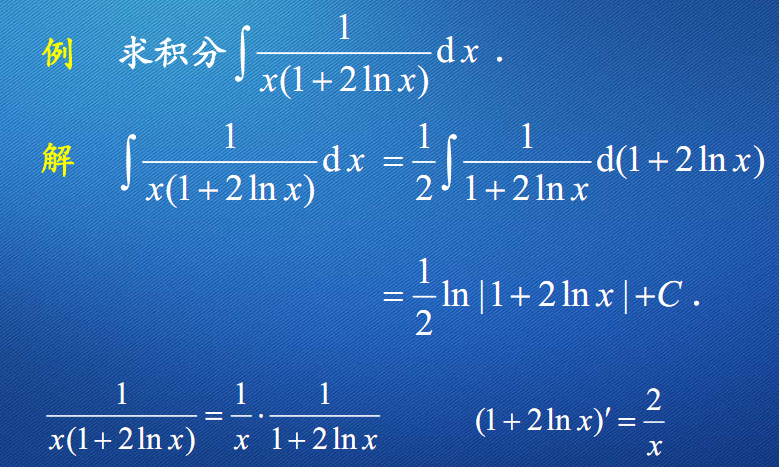



4 3不定积分的第一类换元法 早做准备
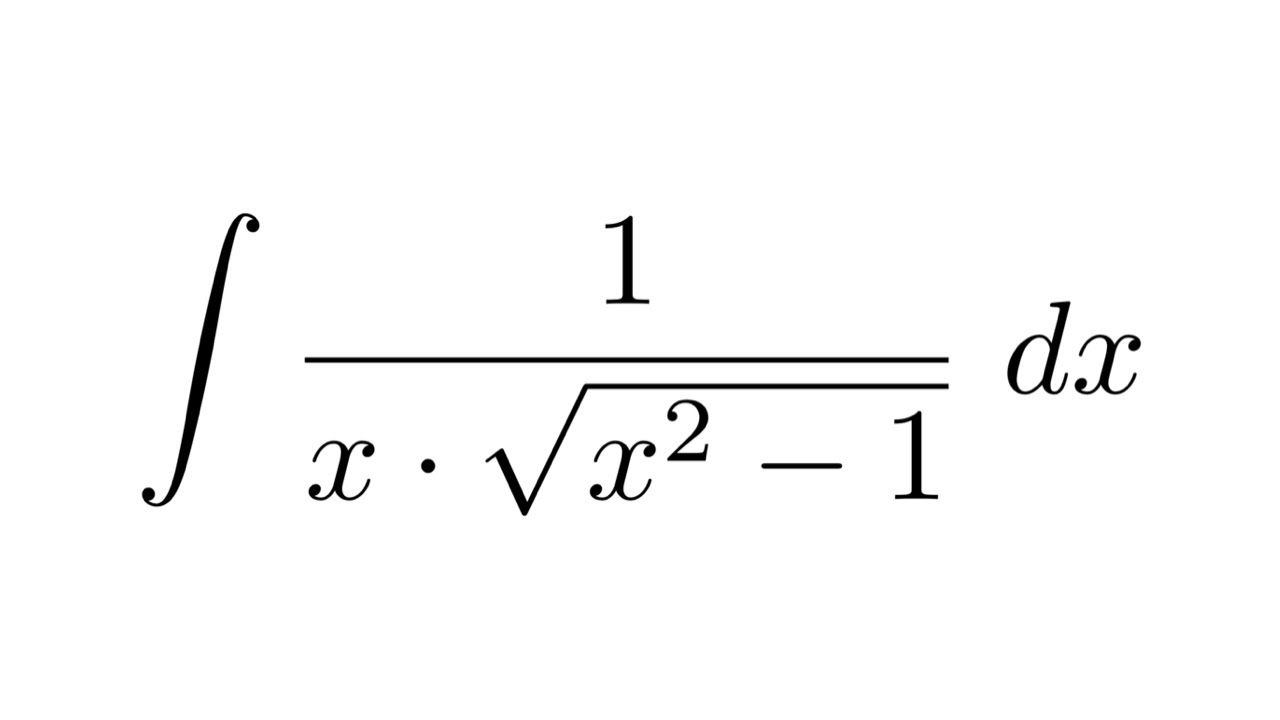



Method 1 Integral Of 1 X Sqrt X 2 1 Substitution Youtube
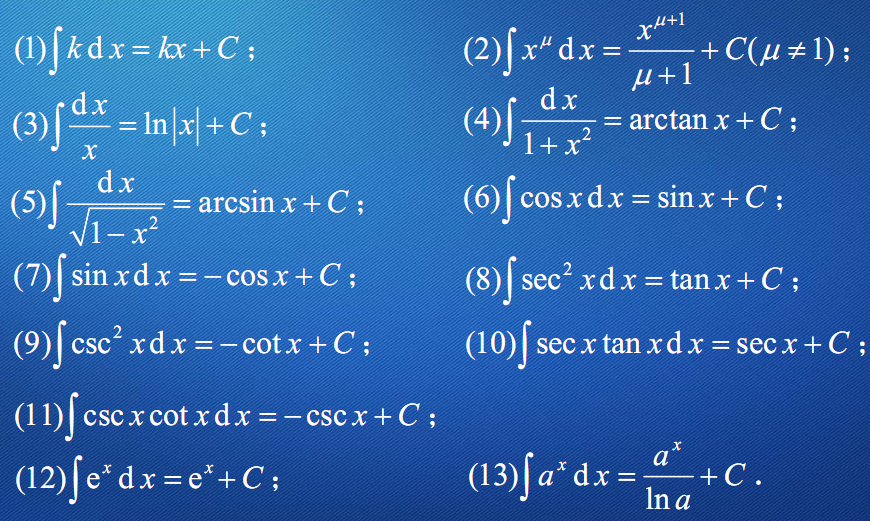



4 2不定积分的性质与基本积分表 早做准备



二重积分计算计算二重积分 领域开拓网



根号下x除以1 X的积分 根号x 1除以x的积分



How To Integrate 4 X 2 1 2 Quora




積分公式 公式種類 不定積分 定積分 其他 公式匯總 不定積分 定積分 積分性質 中文百科全書




求2道积分的1 1 X 根号1 X 2 Dx 2 X 2 4 Xdx 雨露学习互助




How Do You Evaluate Int 0 1 Sqrt X X 2 Dx Socratic




无法求不定积分怎么求定积分 怎么求arcsinx的不定积分 三人行教育网 Www 3rxing Org




How Do You Integrate 1 X 2 Sqrt 1 X 2 Socratic




How Do You Find The Antiderivative Of Int 1 X 2 10x 29 Dx Socratic
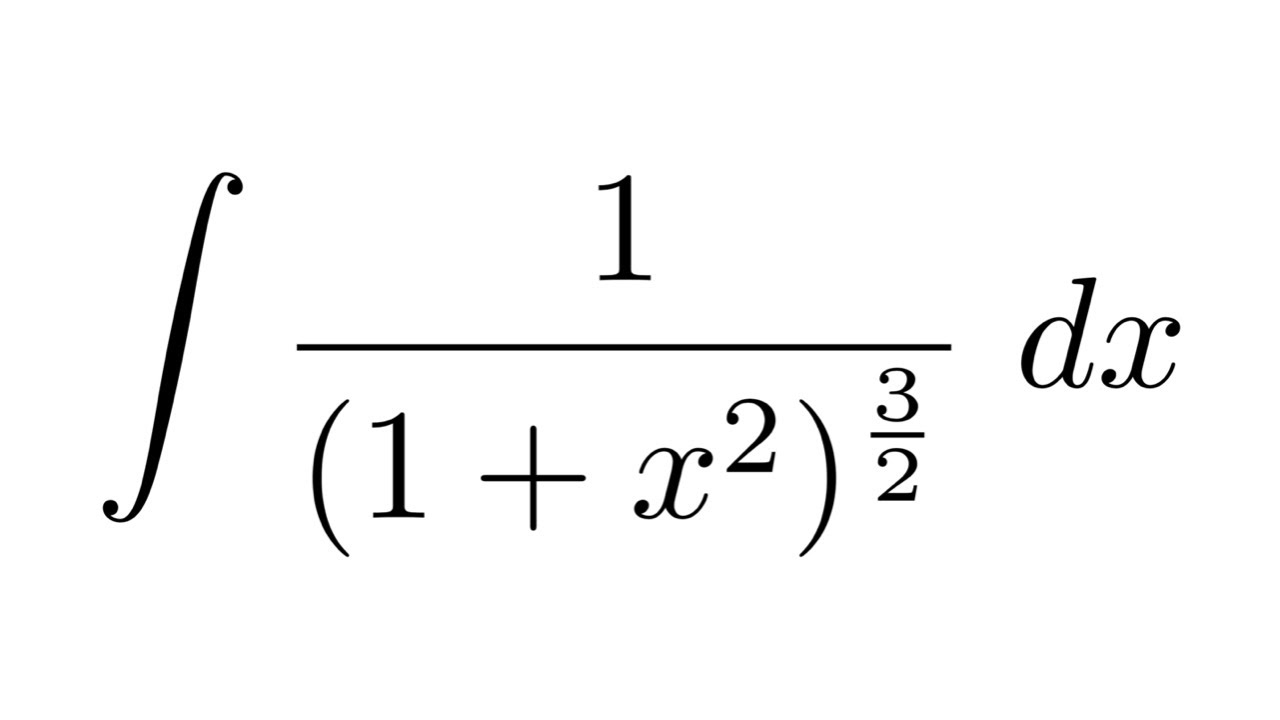



Integral Of 1 1 X 2 3 2 Substitution Youtube



知識家 單元16 5 代換積分 X 1 X Dx A 這是個數學愛好者的樂園 歡迎大家都能夠來分享 思考數學題目 隨意窩xuite日誌




置換積分の方法 置換方法を覚えておきべき積分問題 大学入試数学の考え方と解法



What Is The Integral Of Dx Sqrt X X 2 Quora




Integral Of X 2 Sqrt 1 X Substitution Youtube
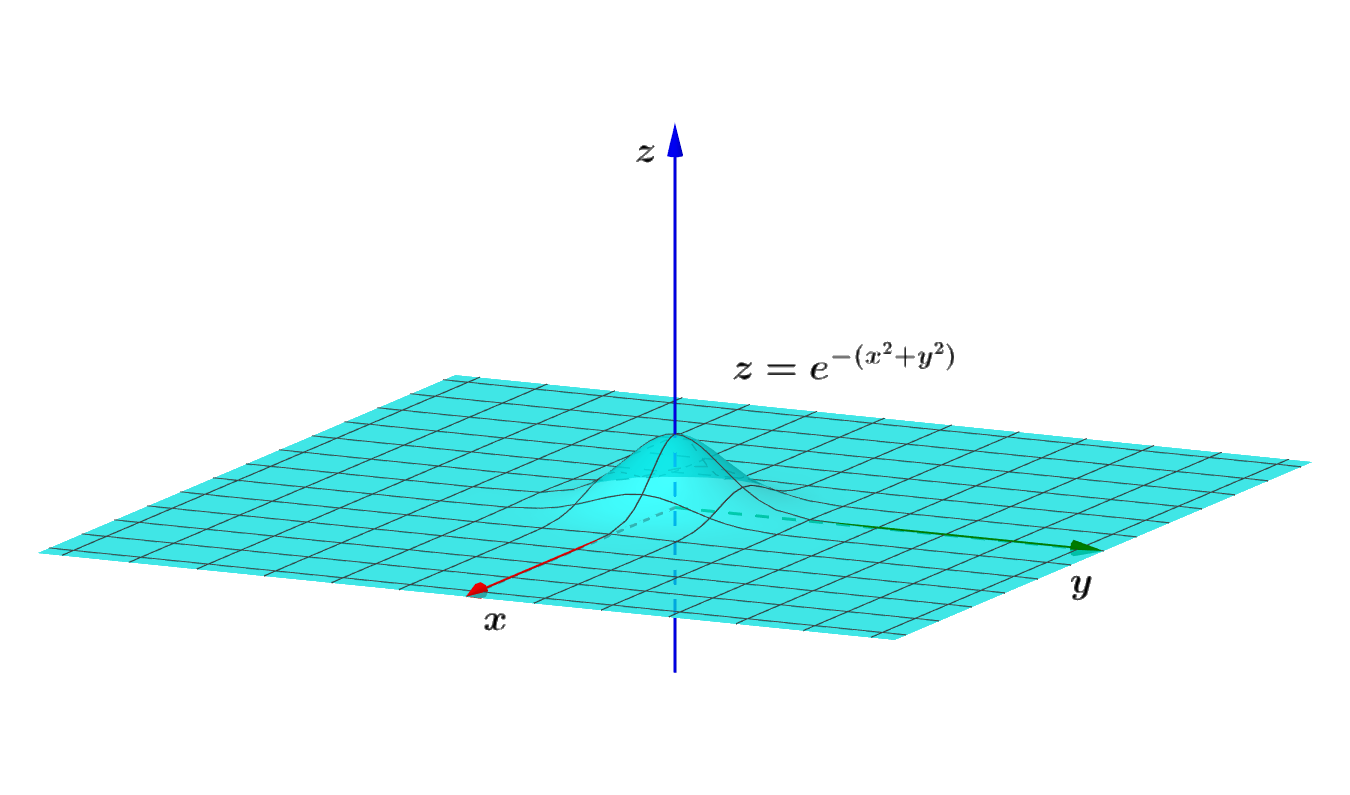



无穷积分 E X 2 Dx 的几种巧妙解法 Blogs Of Zcy1221 Csdn博客




求定积分 上限根号3 下限0 X乘根号下1 X 2 Dx 雨露学习互助




積分 X 1 パターン 完成図の予想 No 021 衒学記鳥の日樹蝶




不定积分x 3 Sqr 1 X 2 3 Dx 雨露学习互助



X2 1 X4 1求不定积分 不定积分 X4 1 X2 1 Dx
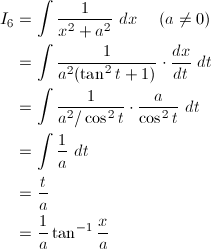



不定積分選 グラフ付き 数学自由研究




Int 1 Sqrt A 2 X 2 Dx Log X Sqrt X 2 A 2 C




How To Integrate 1 X 2 1 2 Quora




實用特殊積分求法 每日頭條




不定积分计算 典型题及解题技巧 上 哔哩哔哩



How To Integrate X 3cosx 2 1 2 Sqrt 4 X 2 Dx For The Interval Of 2 And 2 Quora



Integral Approximations



定积分证明 Dx 1 X 2 X 0 在 X 1 和在 1 1 X 的定积分相等 作业 慧海网



1
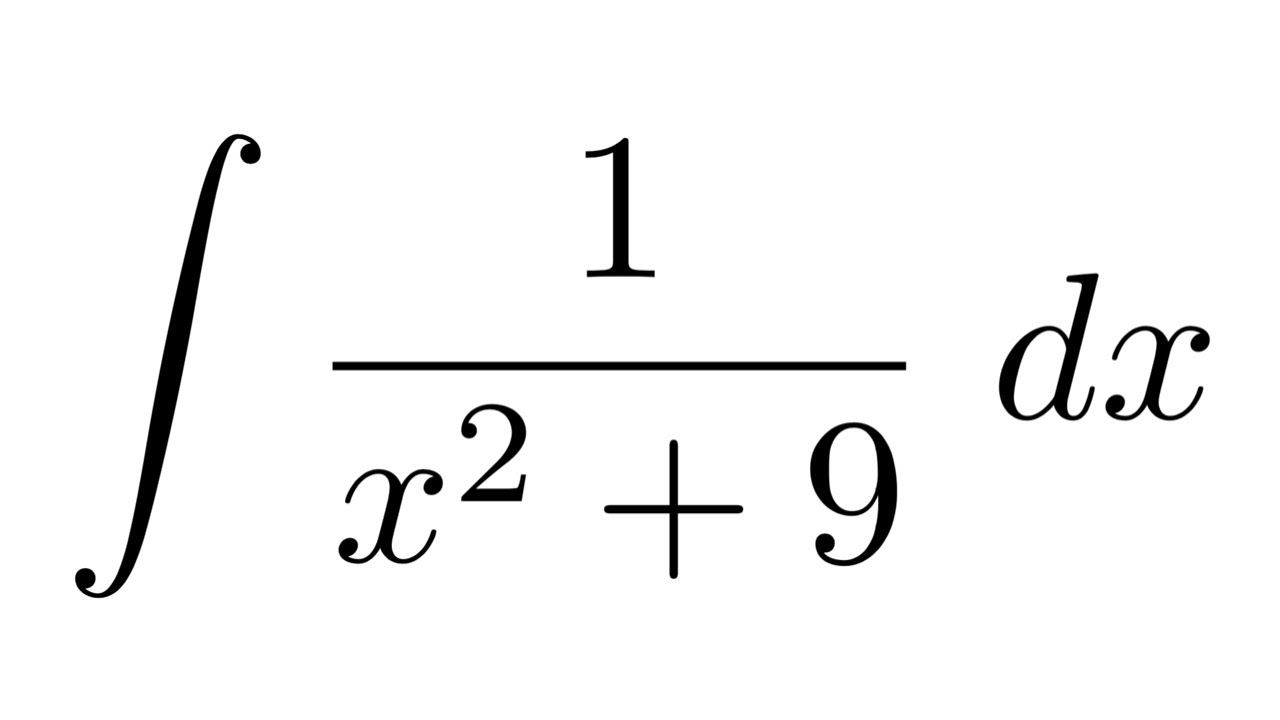



Integral Of 1 X 2 9 Substitution Youtube
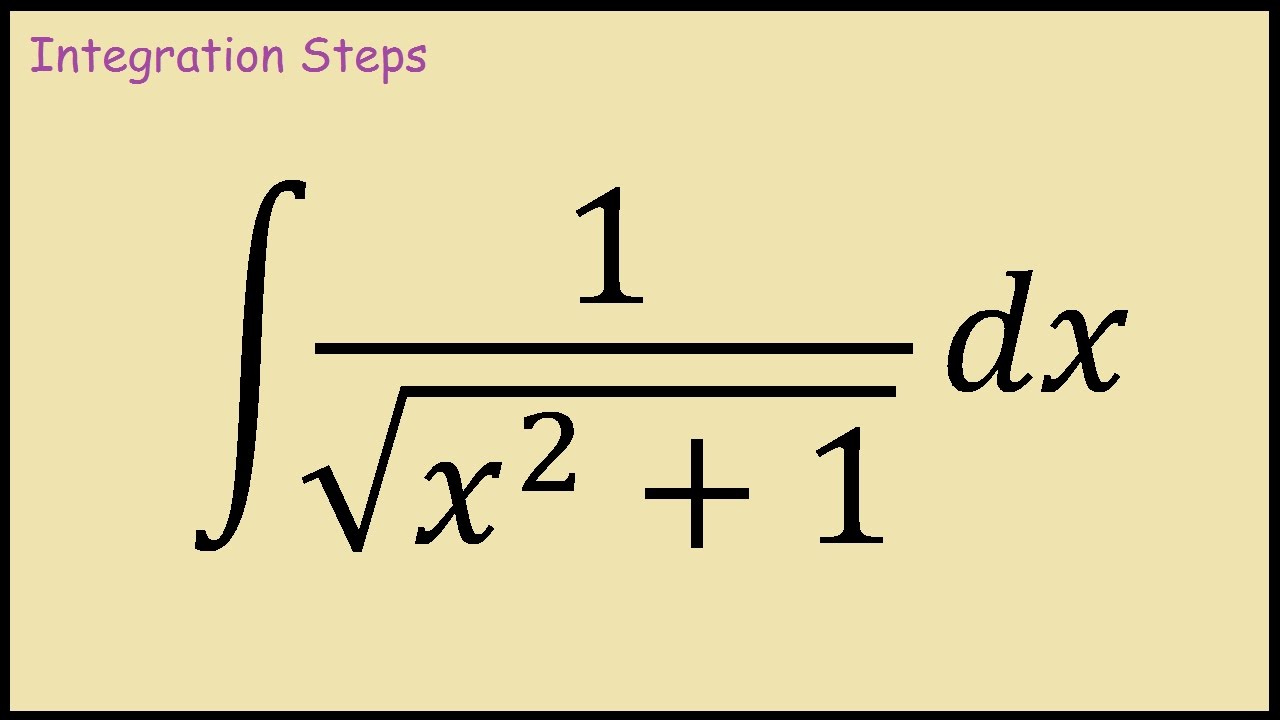



How To Integrate 1 Sqrt X 2 1 Youtube




Ex 7 4 24 Integration Dx X 2 2x 2 Equals A X Tan 1 X 1




标准部分分式的不定积分 Arctanx的不定积分积分 三人行教育网 Www 3rxing Org




求不定积分 Ln 1 根号x Dx 雨露学习互助




Integral Of X 1 X 2 Substitution Youtube
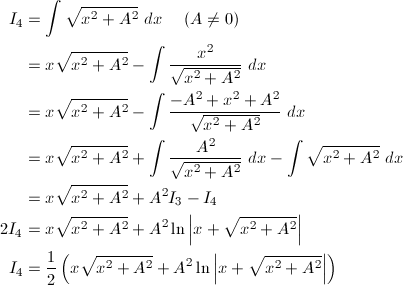



不定積分選 グラフ付き 数学自由研究
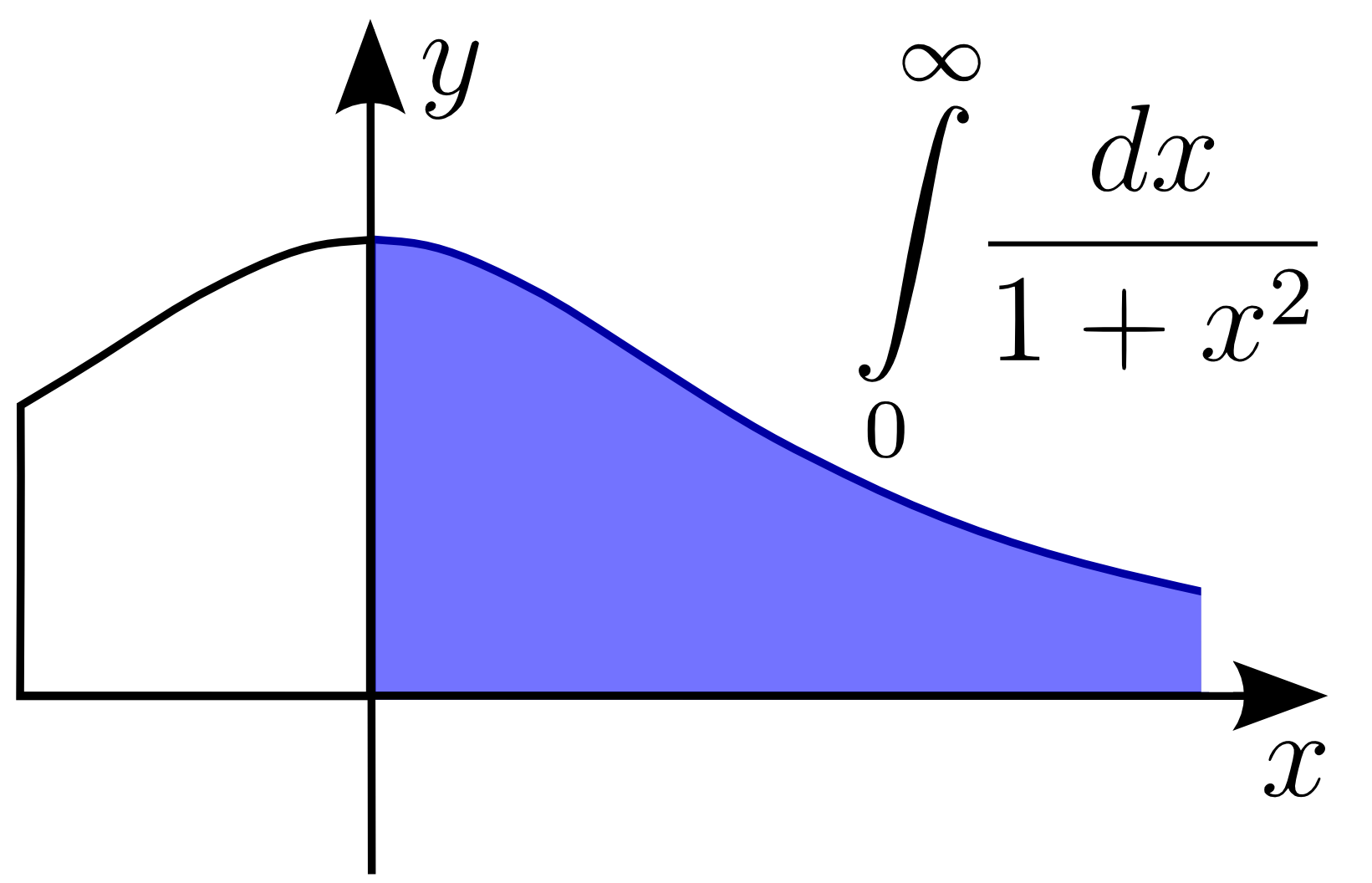



Improper Integral Wikipedia




求不定积分 Xarctanx 1 X 2 Dx 雨露学习互助




怎么解这个不定积分 X 5 X 3 1 X 3 X 2 X 1 Dx 雨露学习互助




怎麼求1 X X 3 的積分 人人焦點



高数求定积分0到1 Ln 1 1 X 2 Dx咋做呀 作业 慧海网




6 2 4 1 部分分式積分法int 1 2x 1 X 1 Dx Youtube




Int 1 Sqrt A 2 X 2 Dx Log X Sqrt X 2 A 2 C




How Do You Find The Antiderivative Of Int Sqrt 9 4x 2 Dx Socratic
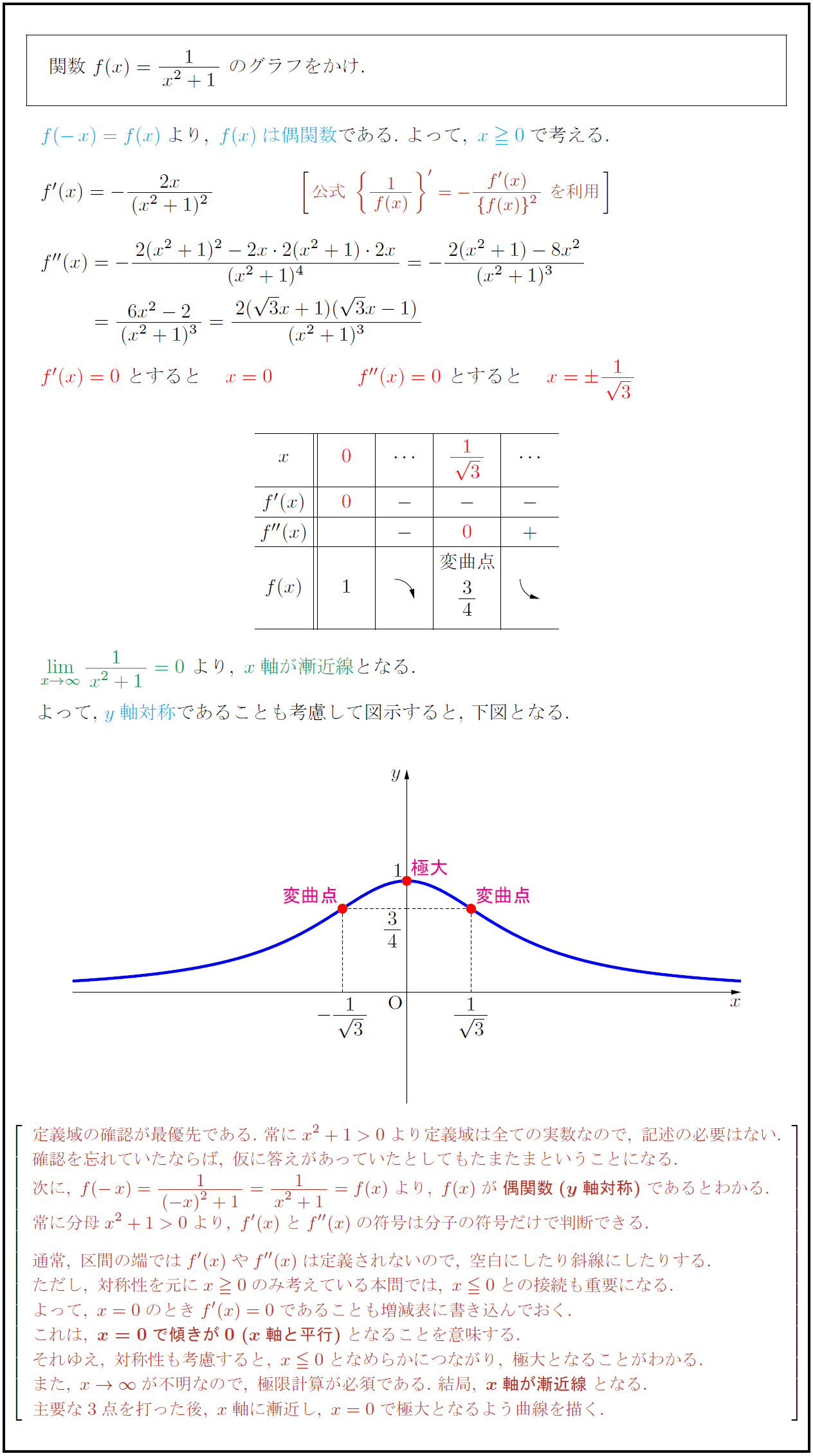



高校数学 分数関数 Y 1 X 1 のグラフ 受験の月



求不定积分 1 X Dx 根号下 1减x的平方 数学解答 作业小助手




曲線弧長




求不定积分 1 二次根号下 E的x次方加二 雨露学习互助



How To Solve The Integral Of X 3 1 X 2 3 Quora




Int 2 2 X 3cos X 2 1 2 Sqrt 4 X 2 Dx



高校数学 特殊な置換をする不定積分 X A を含む不定積分 最高難度 と特殊な置換の根拠 受験の月


コメント
コメントを投稿